
I. Neurosciences et rituels mathématiques
Tous les enseignants sont évidemment d’accord avec le fait que les élèves n’apprennent pas dans l’occasionnel et que seules les activités répétées permettent l’acquisition et l’ancrage des notions. C’est dans mes différentes lectures sur les neurosciences ( Olivier Houdé, Stanislas Dehaene, Steve Masson … ) que j’ai trouvé la confirmation de l’importance, voire de la nécessité, d’instaurer des rituels mathématiques plusieurs fois par jour en maternelle. Je souhaitais donc partager mon expérience sur cette mise en place de rituels
Les activités ritualisées : comment ?
Pour être efficaces en maternelle, elles doivent (à mon sens) répondre à quelques règles.
1. Se dérouler toujours au même moment dans la journée.
Ainsi le cadre est attendu par l’enfant, clairement identifié et donc rassurant. Les notions ne peuvent passer que lorsque le climat de la classe est bienveillant, l’état émotionnel de l’enfant étant un élément clé lors de ces apprentissages.
2. Très important: L’objectif de l’activité doit être clair pour VOUS mais aussi pour L’ENFANT (demandez-vous » pourquoi je fais ça ? Qu’est-ce que j’attends par là ? »)
Parfois, on se surprend soi-même et on s’aperçoit qu’en fait l’activité choisie ou construite n’est pas vraiment adaptée à ce que l’on recherche. Et que les objectifs étant multiples, ils ne sont pas clairement identifiables par l’enfant.
3. L’activité doit avoir un sens.
Par exemple, si on demande à un enfant de compter à l’envers (« à rebours »), cela n’a pas de sens pour lui (en maternelle), car depuis son entrée en PS, on lui demande de réciter la suite numérique dans l’ordre croissant. Par contre, introduire ce rituel en sport lors du départ d’une course, ou d’un relais, prend tout son sens et montre à l’enfant qui donne le départ tout l’intérêt de savoir le faire (5, 4, 3, 2, 1… Partez!)
4. Varier le style de rituel et le temps à y consacrer:
– les rituels peuvent être collectifs (mais tous les enfants doivent passer) lors des regroupements (15 minutes maximun). Dans ces cas-là, je fais passer en premier les enfants les plus à l’aise avec la notion étudiée, afin que les autres enfants puissent observer et se remémorer l’action demandée.
– les rituels peuvent être individuels: J’utilise les interclasses, le moment de sortir en récréation par exemple. Les enfants prêts me donne le « code » (voir exemple de rituels plus loin) pour sortir.
Ces activités ayant pour objectif l’acquisition de notion dans la mémoire à long terme doivent impérativement être en relation avec des activités menées en classe
II. Activités mathématiques ritualisées en lien avec les neurosciences
Le recyclage neuronal est le processus par lequel une région cérébrale est modifiée pour changer sa fonction. Certaines difficultés dans l’apprentissage des nombres peuvent être liées au recyclage neuronal. En effet, d’après Stanislas Dehaene, certaines acquisitions nouvelles, comme le calcul, ne sont possibles « que dans la mesure où elles sont compatibles avec les architectures neuronales préexistantes, qu’elles recyclent ».
Ainsi chaque nouvelle notion doit trouver sa « niche neuronale » dans le cerveau, un « endroit » assez proche que la flexibilité mentale du cerveau permettra de modifier vers une nouvelle fonction.
Ceci se fera en quelques semaines par des activités quotidiennes et répétées.
L’enfant possède dès son plus jeune âge une représentation approximative du nombre. Celle-ci sert de base à l’apprentissage de la numération. Lorsque l’enfant associe chiffres et quantités, il recycle un système préexistant.
Les études de Masson démontrent la plasticité cérébrale et ses conséquences sur les apprentissages et l’organisation du cerveau.
Pour faire simple, lors des apprentissages, notre cerveau établit de nouvelles connexions entre nos neurones. Plus une activité est répétée, plus les nouvelles connexions neuronales sont importantes, donc plus on apprend.
Ceci, contrairement à ce que l’on pensait, se réalise tout au long de notre vie. Naturellement, c’est plus important lors de l’enfance, car le cerveau est en pleine maturation, mais cela reste vrai une fois adulte.
La répétition des apprentissages lors des activités ritualisées est donc essentielle, car elle permet de réactiver de nombreuses fois certaines connexions neuronales (on parle de réactivation neuronale), amenant ainsi notre cerveau à modifier certaines représentations. C’est cette modification qui rendra la notion définitivement acquise.
Il faudra bien entendu consolider les nouvelles acquisitions en les automatisant, afin de modifier durablement la région cérébrale concernée.
Exemple:
Les enfants possèdent une représentation nombre = espace.
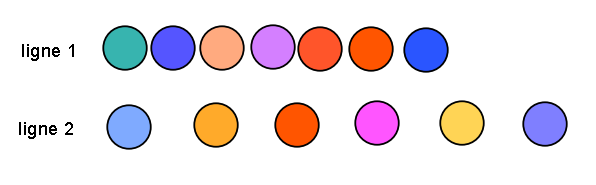
Pour l’enfant, il est tout à fait logique de penser que la ligne 2 compte plus de points. Il faut donc modifier cette représentation grâce à la plasticité cérébrale. Si la plasticité cérébrale est essentielle pour opérer cette modification des architectures neuronales pré existantes, elle ne suffit pas: un autre élément est également indispensable: le contrôle inhibiteur.
L’inhibition cérébrale est la capacité de contrôler, bloquer nos intuitions, nos habitudes, ou nos stratégies spontanées.
Pour reprendre l’exemple précédent, l’enfant doit inhiber sa vision d’une bande plus longue, afin de se concentrer sur la notion de quantité et non de longueur.
Le contrôle inhibiteur est donc un élément fondamental dans la réussite scolaire des enfants.
III. Exemples d’activités ritualisées en mathématiques (en maternelle PS/MS)

Les bases communes à tous les exemples:
Il est d’abord fondamental de donner les bases de la réussite de ces rituels. Ils doivent prendre une place toujours identique dans la journée, pour que cela devienne un repère pour l’enfant. On pourrait dire que le moment choisi est une constante temporelle. L’enfant sait ce qu’on attend de lui, il est rassuré et il a envie d’y participer.
La deuxième constante est le caractère ludique à instaurer pour chaque rituel. C’est essentiel: l’enfant doit le vivre comme un moment de jeu, ce qui augmentera son sentiment de sécurité, afin de ne pas avoir peur « de se tromper »…
Le troisième point important sont les variations à apporter dans les rituels. Le cadre est constant, le caractère ludique est constant lui aussi. C’est la nature du rituel qui devient une variante qui va apporter un aspect encore plus ludique.
Il est essentiel que la règle soit clairement définie avant chaque réalisation du rituel. On la définit ensemble au début de l’activité.
Reste à définir l’objectif de l’enfant face au rituel. C’est la conclusion de la règle du jeu. L’enfant doit penser « J’ai réussi, j’ai gagné… »

Voici ce que j’ai personnellement choisi:
– première constante: les rituels ont lieu lors des moments de sortie en récréation.
– deuxième constante: Pour l’aspect ludique, j’ai instauré un système de code à donner pour pouvoir sortir. C’est la solution au contenu du rituel proposé. Bien entendu, si le code est l’objectif pour les enfants, (je veux sortir!), je gère le jeu afin qu’aucun d’eux ne soit pénalisé par un échec. Chaque code demandé aux enfants est adapté à leurs niveaux, la question est donc individualisée selon le niveau de chaque enfant. Si un enfant donne le « mauvais code » il se met sur le côté afin d’observer les stratégies des autres pour donner le bon code, je lui redemande un autre code par la suite. Les enfants qui rencontrent des difficultés peuvent utiliser diverses aides ( matériel de la classe)
Enfin, j’ai toujours à l’esprit que pour l’enfant, c’est un jeu, et mon attitude de maître du jeu est souvent théâtrale et rythmée.

Exemples de rituel : « Le Code »
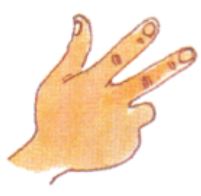
exemple 1:
Cadre: les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maîtresse annonce un chiffre (1, 2, 3, 8… 10) en fonction du stade d’apprentissage de l’enfant.
Code: l’élève doit montrer le nombre de doigts correspondant à la demande.
Objectif: associer constellation et « quantité orale »

exemple 2:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maîtresse n’annonce plus le chiffre mais montre sa représentation écrite.
Code: l’élève doit montrer le nombre de doigts correspondant à la demande.
Objectif: associer constellation et écriture chiffrée.
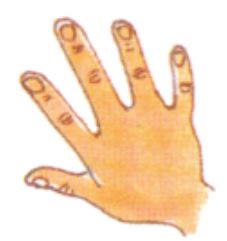
exemple 3:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maître annonce un chiffre
Code: l’élève doit montrer le nombre de doigts correspondant à la demande en utilisant les deux mains. Si la maîtresse annonce 5, l’enfant peut montrer 2 sur une main, et 3 sur l’autre.
Objectif: décomposition d’un nombre.
Aide: des doigts de gants (j’ai découpé de vieux gants en laine, et laissé les doigts qui aideront les enfants dans la décomposition)

exemple 4:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maîtresse montre la carte dé
Code: l’élève doit montrer le nombre de doigts correspondant à la demande.
Objectif: associer constellation dé et doigts. Faire le lien entre les différentes constellations possibles. Notion de la persistance des quantités: 3 doigts, c’est pareil que 3 points, ou que le chiffre 3.
exemple 5:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maîtresse dit un nombre
Code: l’élève doit donner le nombre qui vient après celui annoncé.
Objectif: apprentissage de la comptine numérique.

exemple 6:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maîtresse instaure un dialogue avec l’enfant:
– Combien je te montre de doigts? – 3
Très bien . Maintenant, si j’en rajoute un (sans montrer), combien j’en aurai sur ma main? – 4
Code: l’élève doit donner le nombre qui vient après celui annoncé.
Objectif: calcul mental: lien entre la comptine numérique et le fait de rajouter 1 à chaque fois.
Attention: ces rituels sont vraiment en lien avec le travail fait en classe, sur la frise numérique, où la progression a bien été étudiée pour savoir ce qui se passe quand on rajoute 1

exemple 7:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maîtresse demande de compter pour le départ de la fusée… 5, 4, 3…
Code: l’élève doit compter « à rebours » pour courir jouer.
Objectif: apprentissage de la comptine numérique.
exemple 8:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Règle: la maîtresse montre quelques doigts, et demande à l’enfant d’aider à faire 5. Ex: je montre 3 doigts, l’élève doit montrer le complément, soit 2. L’étape suivante est la vérification en comptant.
Code: l’élève doit deviner le complément à 5
Objectif: commencer à construire la notion de complément.

exemple 9:
Identique à l’exemple 8, mais avec un complément à 10.
exemple 10:
Cadre: Les enfants sont à la queue leu leu, et vont sortir en récréation. Ils doivent pour cela donner le code.
Calcul mental ( 3 + 2 ; 4 + 2; 3 + 3 …) jusqu’à 10…
exemple 11:
Travail sur les dizaines et /ou le sur comptage. 10 + 3; 10 + 4; 10 + 5…
Aide: Affichage en classe. Les enfants peuvent faire des aller retour. Ils gardent en mémoire la question, puis la réponse.




Laisser un commentaire